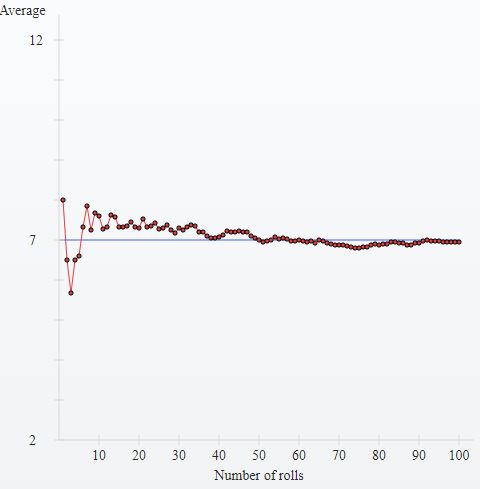
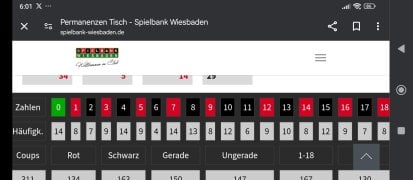
Να ο ένας τρόπος πώς αποδεικνύεται
Ότι όλα τα νούμερα θα ρθουν στους 155 μπιλιές
Κσι ότι σε 37 θα έχουν έρθει 24 νούμερα περίπου πάνω από τα μισά1 φορά
Τα υπόλοιπα 2 ή περισσότερες φορές και 12 δεν θα έχουν έρθει
Δες καλύτερα από το κείμενο που δημοσιεύεται γιατί εμένα δεν μου το παίρνει όλο
Έχει και τα μαθηματικά που αποδεικνύονται αυτά
Some math, and the "law of the third"
www.vlsroulette.com
1 + 37/36 + 37/35 + 37/34 + 37/33
and 6 different numbers:
1 + 37/36 + 37/35 + 37/34 + 37/33 + 37/32
Like I said, it gets tedious calculating all the sums, so I wrote a little program to finish it off:
Number of trials needed to get first number is: 1.00
Number of trials needed to get 2 different numbers is 2.00
Number of trials needed to get 3 different numbers is 3.00
Number of trials needed to get 4 different numbers is 4.00
Number of trials needed to get 5 different numbers is 5.00
Number of trials needed to get 6 different numbers is 6.00
Number of trials needed to get 7 different numbers is 8.00
Number of trials needed to get 8 different numbers is 9.00
Number of trials needed to get 9 different numbers is 10.00
Number of trials needed to get 10 different numbers is 11.00
Number of trials needed to get 11 different numbers is 13.00
Number of trials needed to get 12 different numbers is 14.00
Number of trials needed to get 13 different numbers is 16.00
Number of trials needed to get 14 different numbers is 17.00
Number of trials needed to get 15 different numbers is 19.00
Number of trials needed to get 16 different numbers is 21.00
Number of trials needed to get 17 different numbers is 22.00
Number of trials needed to get 18 different numbers is 24.00
Number of trials needed to get 19 different numbers is 26.00
Number of trials needed to get 20 different numbers is 28.00
Number of trials needed to get 21 different numbers is 30.00
Number of trials needed to get 22 different numbers is 33.00
Number of trials needed to get 23 different numbers is 35.00
Number of trials needed to get 24 different numbers is 38.00
<== This is the "law of the third"
Number of trials needed to get 25 different numbers is 41.00
Number of trials needed to get 26 different numbers is 44.00
Number of trials needed to get 27 different numbers is 47.00
Number of trials needed to get 28 different numbers is 51.00
Number of trials needed to get 29 different numbers is 55.00
Number of trials needed to get 30 different numbers is 60.00
Number of trials needed to get 31 different numbers is 65.00
Number of trials needed to get 32 different numbers is 71.00
Number of trials needed to get 33 different numbers is 78.00
Number of trials needed to get 34 different numbers is 88.00
Number of trials needed to get 35 different numbers is 100.00
Number of trials needed to get 36 different numbers is 118.00
Number of trials needed to get 37 different numbers is 155.00
So you can see that the so-called "law of the third" arises from turning the question around; instead of asking "how many spins are necessary to get all 37 numbers?" you ask "in 37 (or 38) spins, how many different numbers will have not hit" answer - roughly one third.
Notice that although on average, the number of trials needed to get the "full set", is 155, we know that a number can sleep for 300 or more spins, but MOST of the time (68%) they will have all arrived after a similar number of spins to 155.
Το ίδιο μπορούμε να κάνουμε και για στήλες η ντουζίνες
12.00
<== this is the "law of the third"
Number of trials needed to get 9 different streets is 15.00
Number of trials needed to get 10 different streets is 19.00
Number of trials needed to get 11 different streets is 25.00
Number of trials needed to get 12 different streets is 37.00
Notice that the law of the third seems to hold for streets (there are 12 streets, and after 12 spins, one third (4) streets will not have hit, on average). Is there any special significance to the law of the third? No. It's not specific to roulette, but is a general rule. All it says is that the fewer the numbers (or events) there are left to hit, the higher the chance of hitting a number (or event) that has already hit. Nor is there any significance to the "third". You could come up with a "law of the half" or a "law of the sixth", and it would apply equally well to any sequence of trials.
Finally, the 3rd example of 3-pattern EC bets {rrr,bbb,rrb,bbr,rbr,brb,brr,rbb}
1 + 8/7 + 8/6 + 8/5 + 8/4 + 8/3 + 8/2 + 8/1
Number of trials needed to get 1 pattern is: 1.00
Number of trials needed to get 2 different patterns is 2.00
Number of trials needed to get 3 different patterns is 3.00
Number of trials needed to get 4 different patterns is 5.00
Number of trials needed to get 5 different patterns is 7.00
Number of trials needed to get 6 different patterns is 10.00
Number of trials needed to get 7 different patterns is 14.00
Number of trials needed to get 8 different patterns is 22.00
Remember that in this case, a "trial" is not a spin but 3 spins (to make up each pattern).
The general formula for finding the number of trials needed to get the "complete set" of
N equally likely outcomes is:
1 + N[1 + 1/2 + 1/3 + 1/4 + ... + 1/(N-1)]